Region of Interest Algorithms

Region of Interest (ROI) Algorithms

Statistics

This section details the computation of ROI statistics by the ROI Toolkit. The ROI Toolkit provides a high-precision estimate of the following ROI statistics:

Area.
Mean signal intensity.
Standard deviation of signal intensity.
Minimum signal intensity.
Maximum signal intensity.

Line and CurvedLine ROIs have an additional statistic:

Length.

If extended statistics are shown, then the following statistics are computed:

Perimeter.
Minimum Feret's diameter.
Maximum Feret's diameter.

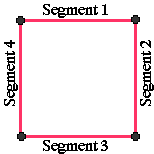
For ROIs that enclose an area, each ROI is defined by the (closed path) outline that encloses the region. For example, in the case of a Rectangular ROI, the outline consists of four line segments joining the four corner points:

To make the computation of ROI statistics feasible, all line segments for an ROI must be straight. So, with Irregular ROIs, what may appear to be a curved outline of the region, is actually made up of many short straight-line segments. This can be seen by zooming into a portion of the Irregular ROI outline.

Elliptical ROIs present a particular problem, since calculation of intensity statistics with a truly curved outline would be problematic and very slow. Calculation of intensity statistics for Elliptical ROIs is therefore done by representing the outline by a series of straight line segments. If the outline is represented by n straight line segments, then the error between the true area of the ellipse and the approximated area is:

(π - (n * sin(π/n) × cos(π/n))) × 100% / π

In Jim versions up to 4.0 n is set to 360 (i.e., for a circular ellipse, each line segment subtends an angle of 1° at the centre), which leads to a difference of 0.005% between the true ellipse area and the area of the ellipse represented by straight line segments. Computation of intensity statistics for ROIs involves multiplying pixel intensities by the the area of pixels that lie with the outline of the ROI. Given a random distribution of pixel intensities with an Elliptical ROI, we therefore expect an error of the order of 0.005% for intensity statistics.

Note: the area statistic returned for an Elliptical ROI is always the true area of the ellipse (= π × semi-major-axis × semi-minor-axis).

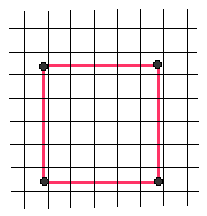
The vertices of an ROI outline may be positioned anywhere with respect to the array of image pixels, so the same Rectangular ROI shown above superimposed on the pixel array may appear like this:

The computation of area and intensity statistics for a generalised ROI composed of straight line segments goes as follows.

Each row of the image is considered in turn.
If the row intersects the ROI anywhere, then each pixel in that image row is considered in turn.
Each pixel is intersected with the ROI.
The total ROI area is the sum of the areas of all the intersected shapes. For Text, Marker and Line ROIs, the area is zero. Let I_i be the intensity of pixel i with non-zero intersected area; let a_i be the intersected area of pixel i; and let A be the total area of all the intersected shapes (i.e., Σ(a_i)).
The mean pixel intensity is
Σ( a_i × I_i) / A.
For a Text or Marker ROI, the mean pixel intensity is the intensity of the pixel at the centre of the text or beneath the marker. Let µ be the mean pixel intensity.
The standard deviation in pixel intensity is:
square root((Σ(a_i × I_i × I_i) - µ × µ × A) / A).
The exception to this is for Text and Marker ROIs, where the standard deviation in pixel intensity is always zero.
Minimum pixel intensity is the minimum intensity in any intersected shape with an area greater than zero. The exception to this is for Text and Marker ROIs, where the minimum pixel intensity is the intensity of the pixel at the centre of the text or beneath the marker.
Maximum pixel intensity is the maximum intensity in any intersected shape with an area greater than zero. The exception to this is for text and Marker ROIs, where the maximum pixel intensity is the intensity of the pixel at the centre of the text or beneath the marker.

The algorithm for Line ROIs is similar to that described above. However, Line ROIs do not enclose any area, and so in the description above substitute "length" for "area".

All shape intersections are performed using the standard Java intersect methods in the java.lang.geom package. Errors in area calculation have been tested for typical and atypically-shaped ROI designed to elicit the largest errors. Errors in the worst cases have been found to be within 1 part in 1000, and for most practical ROIs, errors will be much better than this. These errors are thought not to significantly compromise the validity of results produced by Jim.

Extended Statistics

Perimeter

An ROI's perimeter is defined as follows:

Text and Marker. The perimeter is zero.

Line and Curved Line. The perimeter is defined to be twice the ROI's length.

Rectangular. The perimeter is twice the sum of the width and height of the rectangle.

Elliptical. The perimeter is computed using the YNOT approximation formula, which gives a maximum error of 0.362%. The maximum error occurs when the eccentricity is slightly above 5.
Irregular. The perimeter is the sum of the lengths of the individual straight line segments that make up the ROI.

Feret's Diameters

A Feret's diameter is the separation between a pair of parallel lines that just enclose the ROI, for a particular angle between the parallel lines and (say) the x-axis. As the angle is changed by sweeping through 180°, so the Feret's diameter will change. The minimum and maximum separation of the lines found over all angles are called the minimum and maximum Feret's diameters.

The following generalisations also apply:

The Feret's diameter of Text and Marker ROIs is always zero.
The min. Feret's diameter of a straight Line is always zero, and the max. Feret's diameter is always equal to the length of the line.
The min. and max. Feret's diameters for Rectangular ROIs can be found exactly from Pythagoras' theorem.
The min. and max. Feret's diameters for Elliptical ROIs can be found exactly from the major and minor axis lengths.
For Curved Line and Irregular ROIs, Jim searches for the min. and max. diameters by finding the Feret's diameter for all possible angles, in steps of 1°.

Masking

Masking operations set the pixel intensity values in an image according to whether pixels are inside or outside an ROI or set of ROIs. If more than one ROI is to be used as a mask, then a composite shape is first formed from the union (see the java.lang.geom package) of the individual ROIs.

A pixel is deemed to be inside an ROI if one half or more than one half of the pixel's area is inside the ROI shape.
A pixel is deemed to be outside an ROI if less than one half of the pixel's area is inside the ROI shape.

Contour Intensity

The way that the intensity (level) of a contour is determined from a starting pixel is described here. The starting pixel may have been derived either from a mouse click in the case of without edge detection, or by edge detection as the pixel at the maximum gradient.

The starting pixel at location (i, j) is shown below, and has intensity I_{i, j}.

If the centre of the pixel is considered to be the location of the intensity value, then the interpolated intensities at the four corners of the pixel will be:

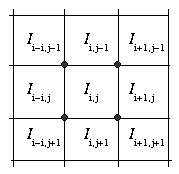
North West Corner Intensity	(I_{i-1, j-1} + I_{i, j-1} + I_{i, j} + I_{i-1, j}) / 4
North East Corner Intensity	(I_{i, j-1} + I_{i+1, j-1} + I_{i+1, j} + I_{i, j}) / 4
South East Corner Intensity	(I_{i, j} + I_{i+1, j} + I_{i+1, j+1} + I_{i, j+1}) / 4
South West Corner Intensity	(I_{i-1, j} + I_{i, j} + I_{i, j+1} + I_{i-1, j+1}) / 4

The contour level is set to the average of the four corner intensities.

Edge Detection

Edge detection can be used to create Irregular ROIs by clicking at a point in the image near an edge. Edge detection finds the strongest edge in the region of the mouse click, and starts contouring from the pixel at the strongest edge location. In Jim versions up to 4.0, the algorithm used to find the edge is described below:

An area 5×5 pixels centred at the location of the mouse click is examined. This is the search area.
For each pixel in the search area (the search pixel), a 5×5 pixel kernel of pixel intensities is formed, centred on the search pixel.
A 2-dimensional surface is fitted (least-squares fit) to the kernel intensity data. The form of the surface is:
y = a + bx + cy.
The maximum gradient of this surface is found as sqrt(b×b + c×c). This is equivalent to the Grad of the surface. This gradient is multiplied by a spatial weighting function that gives greater weight to gradients nearer to the initial mouse click location. The Gaussian weighting factor is:
exp(-(r/5)²),
where r is the distance between the search pixel and the initial mouse click.
The edge location is defined as the pixel within the search area with the biggest weighted gradient of the surface fitted.
The contour intensity at the edge location is determined as for contouring without edge detection.

The constants in the edge detection algorithm (for the search area, kernel size, and spatial weighting function) were determined by trial and error to give good results when outlining brain lesions.

Jim Home